RightEdge Systems Information

RightEdge was a trading system development platform based on modern, compiled languages. It was used to design, develop and backtest trading systems. RightEdge could be used to execute fully automated trading systems. This platform was equipped with a cutting edge integrated development environment (IDE) that included advanced charting features, a full library of technical indicators, data management, and a pluggable architecture that allowed for a high level of scalability and customization. Built trading systems for stocks, futures, options and forex.
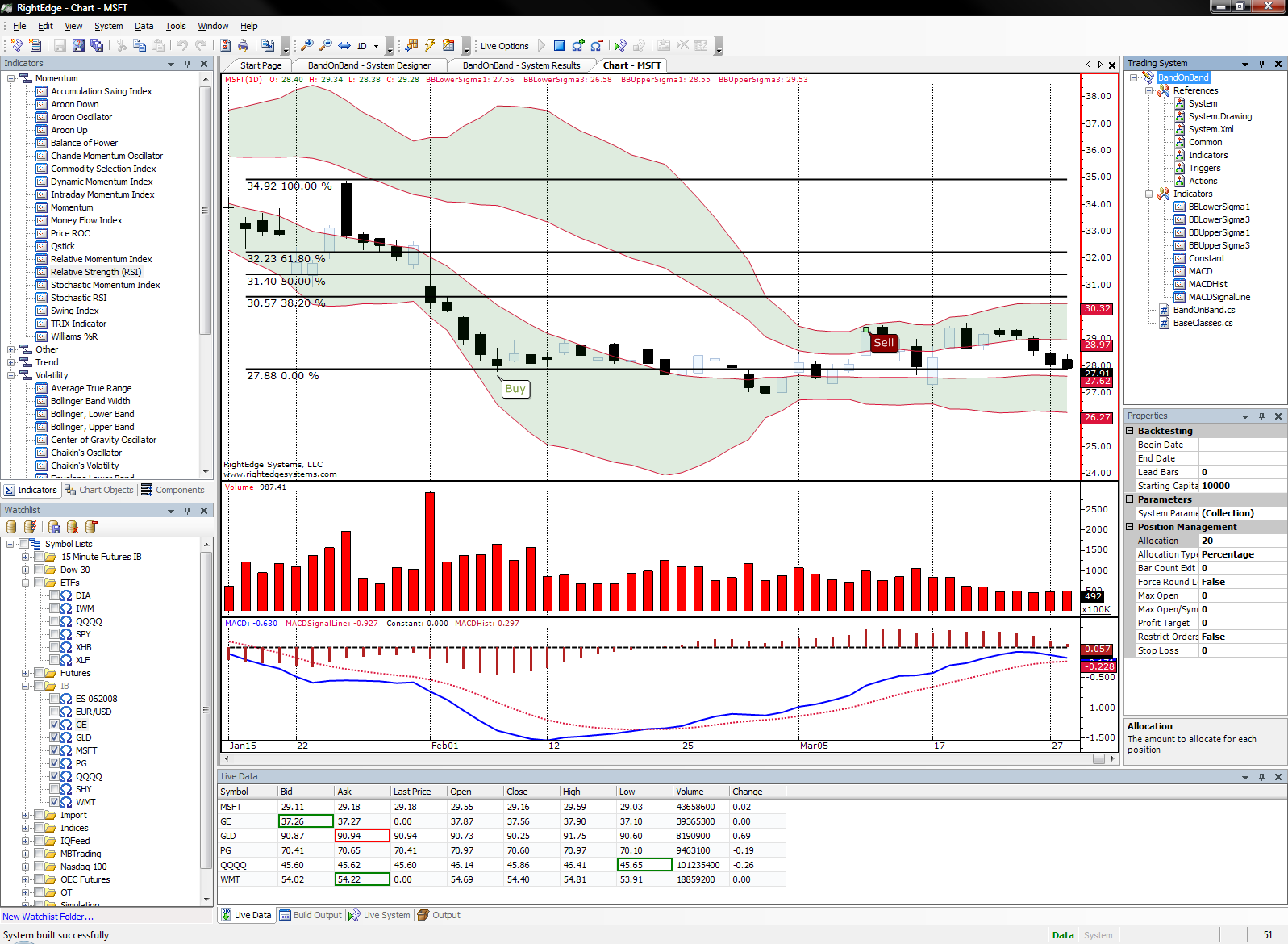
RightEdge supported multiple time frames so that it was valuable to both day traders as well as swing traders. With powerful charting, technical indicators and array of objects such as Fibonacci lines, support and resistance and more, RightEdge was also appealed to those who perform demanding technical analysis.
RightEdge catered to trading system developers that demand high performance systems utilizing industrial strength data storage for high frequency data. Once a trading system was developed, RightEdge could backtest trading systems, made optimization recommendations, and ultimately interfaced with supported brokers to execute automated trading systems live. Trading systems were executed in a truly event driven fashion allowing for the same code to be run in a backtest (simulation) or live scenario.
It worked on the website rightedgesystems.com, but now it belongs to MomTubeVideos.com group that offers lots of mom sex videos and related content for adults on this tube.